

Therefore, the correlation x and y would be unchanged after a linear transformation. A linear transformation preserves linear relationships between variables. Generally, there are two kinds of transformations. What is a Transformation to Achieve Linearity?Ĭonverting a variable involves using a mathematical operation to change its measurement scale. Once a residual plot data set to be nonlinear, it is commonly possible to "transform" the raw data to make it more linear and it will allow us to use linear regression techniques more effectively with nonlinear data. It means that the errors the model makes are not consistent cross-ways variables and observations (ie. Non-normality or non-random of the residual plot is an indication of an inadequate model.

The above last two patterns are non-random (U-shaped and inverted U), suggesting a better fit for a nonlinear model.
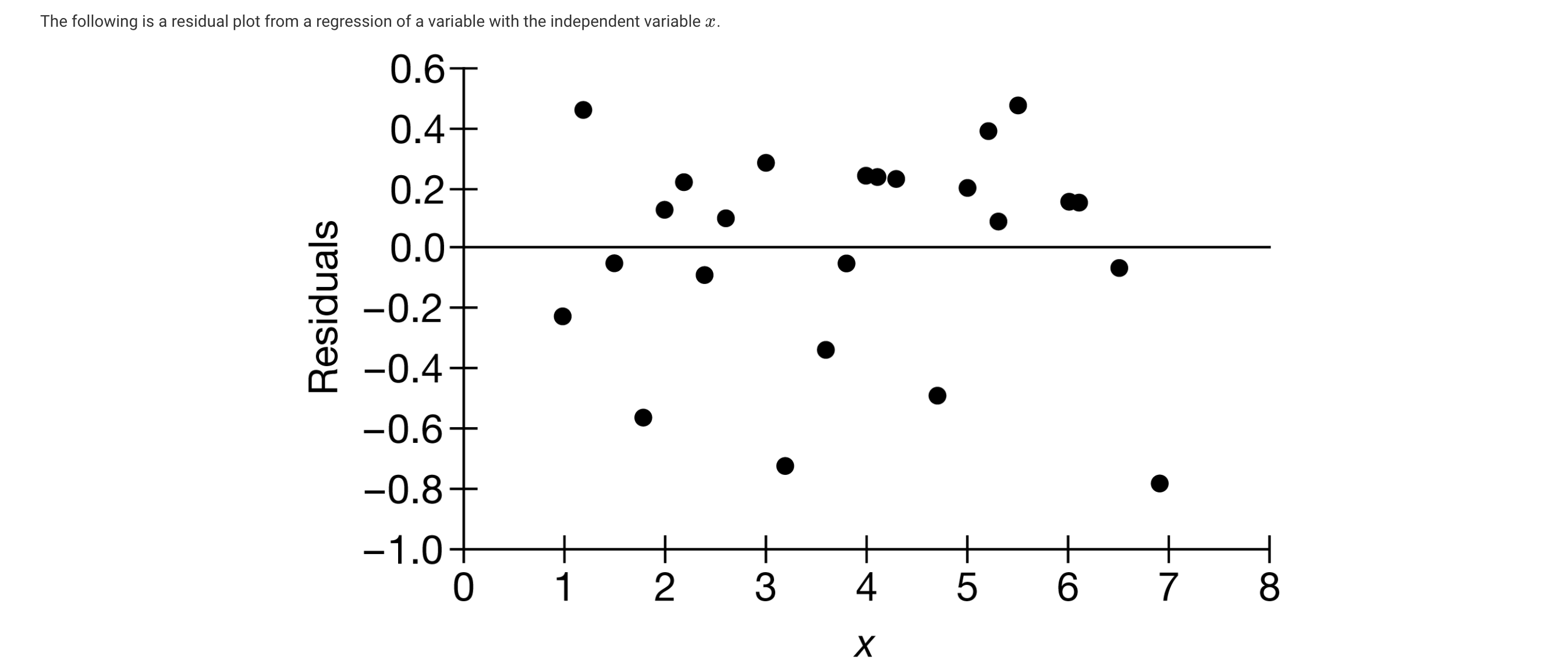
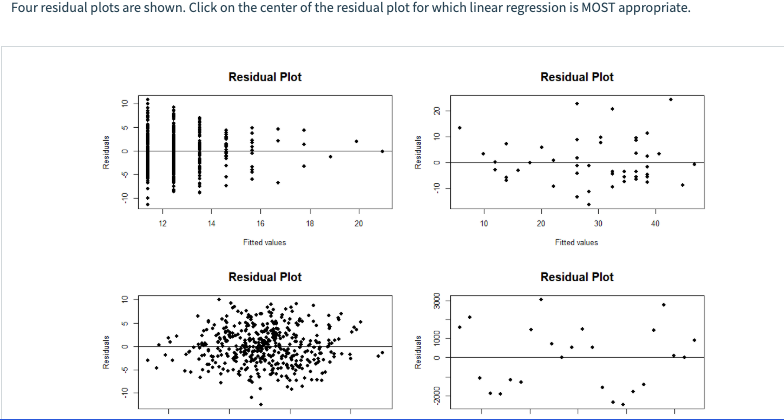
The following first plot shows a random pattern, indicating a good fit for a linear model. This random pattern is clearly indicating that a linear model provides a moderate fit to the data.īelow, the residual plots show three typical patterns for the reference. The above residual plot shows a fairly random pattern, the first residual is positive and then the next two residuals are negative, the fourth one is positive residual, and the last residual is negative. The below chart displays the residual (e) and independent variable (X) as a residual plot. The below table shows the inputs and outputs from a simple linear regression analysis. The facts in a residual plot are randomly dispersed around the horizontal axis, then linear regression model is mostly appropriate for the particular data set otherwise, a nonlinear model is more appropriate. Together the sum and the mean of the residuals are equal to zero ( Σ e = 0 and e = 0).Ī residual plot is a chart that shows the residuals on the vertical axis and the independent variable on the horizontal axis. Residual (e) is the difference between the observed value of the dependent variable ( y) and the predicted value ( ŷ) and each data point has one residual. Since a linear regression model is not always appropriate for the data, you should assess the appropriateness of the respective model by defining residuals and examining residual plots. The difference between the height of each person in the sample and the observable sample mean is a residual.The difference between the height of each person in the sample and the unobservable population mean is a statistical error, whereas.The division is most important in regression analysis, where the concepts are sometimes called the regression statistical errors and regression residuals and where they lead to the concept of studentized residuals. The Error of an observed value is the deviation of the observed value from the true value of quantity of interest (for example: a population mean) and the residual of an observed value is the variance between the observed value and the estimated value of the quantity of interest (for example: a sample mean). Residual = Observed value - Predicted value Q 271. What is a residual in Regression? Why is it important to analyze the residuals before assessing the goodness of a Regression Model? What does it mean if Residuals are non normal or non random?Ĭutting-edge statistics and optimization, Residuals and statistical errors are closely related and easily disordered measures of the deviation of an observed value of an element of a statistical from its “Theoretical Value”.


 0 kommentar(er)
0 kommentar(er)
